Teilchen oder Welle – Das ist hier die Frage!

Der Welle-Teilchen-Dualismus

Die Eigenschaft von Licht bzw. elektromagnetischen Wellen und von Teilchen, jeweils als Wellenphänomen oder als Teilchenphänomen in Erscheinung zu treten, ist als sog. Welle-Teilchen-Dualismus bekannt.
Dieser Dualismus führte schließlich zur Einführung der Quantenmechanik durch Heisenberg, Bohr, Jordan u.a. Anfang der 1930er Jahre. Das Wesen der Quantenmechanik liegt in der berühmten Unschärferelation, die besagt, dass der Ort x und Impuls p eines physikalischen Objekts gleichzeitig nur mit einem Messfehler (Unschärfe) in der Größenordnung der Naturkonstante h (Plancksches Wirkungsquantum) bestimmt werden können.
Erstaunlicherweise findet man heute noch in vielen Lehrbüchern die Ansicht vertreten, die Unschärfe sei grundsätzlich mit dem Messprozess verbunden. Dies ist ein Irrtum, dem übrigens auch Heisenberg selbst erst unterlag, aber durch Bohr darauf hingewiesen wurde, dass die Unschärfe eines Objekts von intrinsischer Natur, also dem Objekt zueigen und unabhängig vom Messprozess ist.
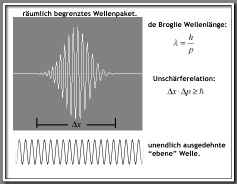
Beschreibt man ein Objekt, z. B. ein Elektron, durch eine Welle, wird diese Unschärfe sofort anschaulich. Genau genommen beschreibt man ein Objekt nicht durch eine Welle, sondern durch viele sich überlagernde Wellen, die ein Wellenpaket bilden.

Ein physikalisches Objekt mit einer Masse ungleich Null nimmt mit 100%iger Wahrscheinlichkeit einen bestimmten Raumbereich ein. Befindet sich z. B. ein Elektron in einem Metallfaden, dann liegt die Wahrscheinlichkeit, das Elektron außerhalb des Metallfadens aufzufinden, bei 0%. Analog dazu muss man also im Wellenbild eine Form finden, die dem Elektron immer einen bestimmten Raumbereich zuweist, der der Größe des Elektrons entspricht.
Die Form einer einzelnen Welle ist dazu nicht in der Lage, da eine solche sog. ebene Welle kein Anfang und kein Ende hat. Ein Wellenpaket dagegen nimmt nur einen begrenzten Raumbereich ein. In der nicht-quantenmechanischen klassischen Physik befände sich das Elektron an einem genau bestimmten Ort x. Das wäre insofern etwas merkwürdig, da das Elektron ja eine räumliche Ausdehnung hat und daher eigentlich nur innerhalb eines bestimmten Ortsbereichs sein kann. In der klassischen Physik ist dies aber kein Widerspruch, sondern dort können, so hat es bereits Newton gezeigt, die Orte physikalischer Objekte durch die Koordinaten ihrer Massenschwerpunkte beschrieben werden. Ein Fußball kann also am Ort x sein, womit gemeint ist, der Masseschwerpunkt des Balls befindet sich exakt an den Koordinaten des Ortes x. Im Wellenbild der Quantenmechanik kann das Elektron bzw. der Masseschwerpunkt des Elektrons prinzipiell aber nur bis auf die Breite Δx des Wellenpakets des Elektrons genau bestimmt werden. Somit bleibt immer eine gewisse Ortsunschärfe Δx.
Die Eigenschaften der Welle bzw. des Wellenpakets, die einem Teilchen zugeordnet werden können, werden durch die de Broglie-Wellenlänge und Frequenz charakterisiert.
Umgekehrt werden die Teilcheneigenschaften einer Welle durch die de Broglie-Formulierung festgelegt. Ein Photon mit der Wellenlänge λ kann auch als Teilchen mit der de Broglie-Wellenlänge λ verstanden werden.
Da sich ein Photon immer mit Lichtgeschwindigkeit c bewegt, hat es im Gegensatz zum Elektron keine Ruhemasse, d. h., man kann ein Photon nicht einfangen und auf eine Waage legen, ein Photon existiert nur, solange es mit c dahinrast.
Gemäß der Einsteinschen Relativitätstheorie unterscheidet man zwischen Ruhemasse und bewegter, träger Masse. Nur Objekte, deren Ruhemasse gleich Null ist, können sich demnach mit Lichtgeschwindigkeit bewegen.
Zur Beschreibung der de Broglie-Wellenlänge des Photons benötigt man daher auch kein Wellenpaket, sondern nur eine Welle mit Wellenlänge λ ist ausreichend.