Geburt der Schwarzen Löcher aus Einsteins Theorie

Fast jeder hat schon einmal von Schwarzen Löchern gehört, diesen mysteriösen Objekten, die sich in einer Vielzahl im Universum befinden sollen, so auch im Zentrum unserer eigenen Galaxie, Objekte, deren Masse sich in einem winzigen Volumen zusammenballt, mit einer solch großen Anziehungskraft, dass sie alles, was in ihre unmittelbare Nähe gelangt, unwiederbringlich in sich aufsaugen, selbst Licht.

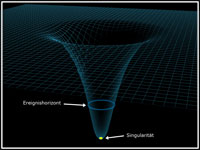
Doch wer versteht wirklich, was es mit diesen bizarren Objekten auf sich hat? Dies hängt wohl auch damit zusammen, dass der Name bereits missverständlich, wenn nicht gar irreführend ist. Bei einem schwarzen Loch handelt es sich nicht um ein Loch im eigentlichen Sinne. Ein solches Objekt ist auch nicht wirklich schwarz. Ein Schwarzes Loch zeichnet sich vielmehr dadurch aus, dass es vor allem eine substanzielle Eigenschaft besitzt, nämlich Masse, und diese ist auf einen unendlich kleinen und dichten Punkt, die Singularität, konzentriert. An der Singularität wird auch die Gravitationskraft unendlich gross. Die Anziehungskraft eines solchen Objekts ist so groß, dass alles, was in seine unmittelbare Nähe innerhalb eines bestimmten Bereichs, des sog. Ereignishorizonts, gerät, derart stark angezogen wird, dass es unwiederbringlich vom Schwarzen Loch verschlungen wird. Da auch Licht, welches diese Grenze überschreitet, nicht mehr entweichen und zum Beobachter gelangen kann, würde uns das Objekt schwarz erscheinen, wenn wir es denn beobachten könnten. Eigentlich können wir es aber überhaupt nicht sehen. Alles, was innerhalb des Horizonts eines Schwarzen Lochs liegt – also auch die Singularität -, wird für uns Menschen für alle Zeiten verborgen bleiben, so stark wir uns auch anstrengen mögen, das Objekt theoretisch zu verstehen. Und trotzdem oder gerade weil sie so geheimnisvoll sind, stellen Schwarze Löcher eine der ultimativen Herausforderungen der modernen Physik dar.

So wie die meisten Physiker und Astronomen glauben, führt der Kollaps eines genügend massereichen Sterns am Ende seines Lebens, wenn all sein nukleares Brennmaterial aufgebraucht ist und kein Gegendruck mehr zur den Stern zusammenziehenden Gravitationskraft besteht, zu der Entstehung eines Schwarzen Lochs. Nach dieser Vorstellung kollabiert der Stern solange, bis alle Masse innerhalb eines unendlich kleinen und somit unendlich dichten Punkts komprimiert ist. Ähnlich wie zum Zeitpunkt des Urknalls das gesamte Universum in einem unendlich kleinen und dichten Punkt konzentriert sein soll, so kann man sich vorstellen, dass auch die gesamte Masse des Schwarzen Lochs in einem unendlich kleinen Punkt konzentriert ist. In dieser Singularität, die ein mathematisches Phänomen darstellt, steckt die gesamte Masse eines Schwarzen Lochs. Und diese stellt auch die Quelle der Gravitation eines Schwarzen Lochs dar.

Die Grenze des Schwarzen Lochs zum restlichen Weltall stellt der Ereignishorizont dar, der die Singularität und damit das Innere des Schwarzen Lochs vor der Außenwelt verbirgt, aber nicht als Oberfläche desselben verstanden werden darf, die es nicht hat. Alles, was von außen diesen Horizont überschreitet, selbst Licht, kann das Schwarze Loch nie mehr verlassen. Dieser Ereignishorizont definiert sich über den sog. Schwarzschild-Radius benannt nach dem Astrophysiker Karl Schwarzschild, der ihre Existenz vorhersagte. Dieser Radius ist proportional zur Masse des Schwarzen Lochs. Je größer also die Masse, desto größer ist auch die Ausdehnung des Objekts. Würde man etwa die Sonne zu einem Schwarzen Loch umfunktionieren wollen mit der Masse der Sonne von 2 mal 10³⁰ kg, so müsste man diese soweit komprimieren, dass von dem ursprünglichen Radius der Sonne von 700.000 km nicht mehr viel übrig bliebe. Man erhielte ein Schwarzes Loch mit einem Radius von nur 3 km. Unsere Erde wäre dagegen vergleichsweise noch winziger. Ihr Radius würde gerade einmal 1 cm betragen.